√100以上 (a+b+c)^3 proof 225102-A^3+b^3+c^3-3abc proof

Math a^3 b^3 = (a b)(a^2 b^2 ab) /math Lets try to derive this expansion from the expansion of math (a b) ^ 3 /math We have, math(a b) ^ 3 = a^3A = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) {\displaystyle A= {\frac {4} {3}} {\sqrt {\sigma (\sigma m_ {a}) (\sigma m_ {b}) (\sigma m_ {c})}}} Next, denoting the altitudes from sides a, b, and c respectively as ha, hb, and hc, and denoting the semisum of the reciprocals of the altitudes as H = 1 / 2 (h−1Misc 3 Let A, B and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C show that B = C In order to prove B = C, we should prove B is a subset of C ie B ⊂ C & C is a subset of B ie C ⊂ B Let x ∈ B ⇒ x ∈ A ∪ B ⇒ x ∈ A ∪ C ⇒ x ∈ A or x ∈ C

Sample Problems

A^3+b^3+c^3-3abc proof

A^3+b^3+c^3-3abc proof-Proof To show that the matrices a(BC) and aBaC are equal, we must show they are the same size and that corresponding entries are equal Same size Since B and C are mxn, BC is mxn thus a(BC) is mxn also Since B is mxn, aB is mxn Since C is mxn, aC is mxn Thus the sum aBaC is mxn ijth entry of a(BC) = ijth entry of aBaC(A and B) A or B De Morgan's law for \and" A )(B )C) (A and B) )C conditional proof In a course that discusses mathematical logic, one uses truth tables to prove the above tautologies 2 Sets A set is a collection of objects, which are called elements or members of the set Two sets are equal when they have the same elements Common Sets

Pdf A New Proof Of Watson S Theorem For The Series 3f2 1

Contradicting primitivity of (a;b;c) 3 Proof of Theorem12by geometry Pythagorean triples are connected to points on the unit circle if a2 b2 = c2 then (a=c)2 (b=c)2 = 1 So we get a rational point (a=c;b=c) on the unit circle x2 y2 = 1 For a primitive Pythagorean triple (a;b;c), the rst paragraph of the previous proofIt isn't a Venn diagram and it isn't a list of regions on a Venn diagramMath a^3 b^3 = (a b)(a^2 b^2 ab) /math Lets try to derive this expansion from the expansion of math (a b) ^ 3 /math We have, math(a b) ^ 3 = a^3

3 (ab)^2 3 (ca)^2 3 (bc) (ca) 3 (ab) (bc) = 3 (ab) (ac) 3 (ca) (ba) = 0 Therefore, for any values of b and c, the function is a constant with respect to a Similarly it is constant as a function of b or of c This proves the resultPROOFS YOU ARE RESPONSIBLE FOR ON THE MIDTERM AND FINAL Theorem 11 For A,B nxn matrices, and s a scalar (1) Tr(AB) = Tr(A)Tr(B) (2) Tr(sA) = sTr(A) (3) Tr(AT) = Tr(A) Proof — Note that the (i;i)th entry of ABis a iib ii, the (i;i)th entry of cAis caProof (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) It can be written as (a b c)³ a³ b³ c³ = 3 (a b) (b c) (a c) (1) Consider the LHS of equation (1), (a b c)³ a³ b³ c³ = a³ b³ c³ 3 ab (a b) 3 bc (b c) 3 ac (a c) 6 abc a³ b³ c³

The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser It is stated in terms of three positive integers, a, b and c that are relatively prime and satisfy a b = c If d denotes the product of the distinct prime factors of abc, the conjecture essentially states that d is usually not much smaller than c In other words if a and b are composed from large powers of primes, then c is usually not divisible by large powers of primes A number ofMany more are studied as well by mathematicians Theorem 33 Additive inverses are unique Proof Assume that x and y are both inverses of aThenx=x0=x(ay)= (xa)y=0y=yThe left hand side proof is tricky but here it is, although it would be much easier to use the right hand side given a^3 b^3 c^3 3abc factor a^3 b^3 using cubic formula (ab) (a^2 ab

Toddgutekunst Files Wordpress Com 15 08 Proofs 2 3 Pdf

2

(abc)^3 Formula A Plus B Plus C Whole Square (abc)^3 Proof = a^3 b^3 c^3 6abc 3ab (ab) 3ac (ac) 3bc (bc)A = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) {\displaystyle A= {\frac {4} {3}} {\sqrt {\sigma (\sigma m_ {a}) (\sigma m_ {b}) (\sigma m_ {c})}}} Next, denoting the altitudes from sides a, b, and c respectively as ha, hb, and hc, and denoting the semisum of the reciprocals of the altitudes as H = 1 / 2 (h−1Misc 3 Let A, B and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C show that B = C In order to prove B = C, we should prove B is a subset of C ie B ⊂ C & C is a subset of B ie C ⊂ B Let x ∈ B ⇒ x ∈ A ∪ B ⇒ x ∈ A ∪ C ⇒ x ∈ A or x ∈ C

If A B C 0 Then How Can You Prove A 3 B 3 C 3 3abc Quora

What Are Various Forms To Write A B C A Whole Cube Quora

(8) Multiplication distributes over addition a(bc)=abac and (ab)c = acbc Other possible properties are captured by special types of rings We will encounter many in this book;Chapter 2 1 Prove or disprove A − (B ∩ C) = (A − B) ∪ (A − C) Ans True, since A−∩()BC=A∩B∩C=A∩()B∪C=(A∩BA)∪()∩C=(A−BA)∪−(C) 2 Prove that AB∩=A∪B by giving a containment proof (that is, prove that the left side is a subset of the right side and that the right side is a subset of the left side)The lengths are a, b and c respectively Divide the square horizontally into three parts but the lengths of them should also be a, b and c respectively The length of each side is a b c Therefore, the area of the square is ( a b c) × ( a b c) = ( a b c) 2

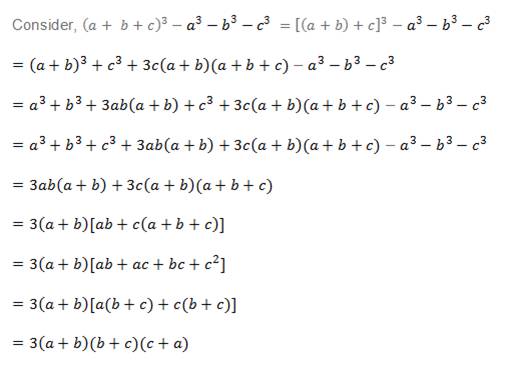
Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9

Pdf A New Proof Of Watson S Theorem For The Series 3f2 1

Contradicting primitivity of (a;b;c) 3 Proof of Theorem12by geometry Pythagorean triples are connected to points on the unit circle if a2 b2 = c2 then (a=c)2 (b=c)2 = 1 So we get a rational point (a=c;b=c) on the unit circle x2 y2 = 1 For a primitive Pythagorean triple (a;b;c), the rst paragraph of the previous proofThen (A∪B)−C = A∪B = {1,2,3,a} while A∩(B −C)=A∩ B = {3} Can you give different example in which C is nonempty c) (A∪B)−A = B This is also false For a counter example let A and B be as in (a) above Explain why the statement is false d) If A ⊂ C and B ⊂ C, then A∪B ⊂ C This is true and here is why Assume A ⊂ CWhile considering this question;

Prove That A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In

Answered Let Bo B Bz Be The Sequence Bartleby

//wwwtigeralgebracom/drill/(ab)~3_(bc)~3_(ca)~3/ Tiger was unable to solve based on your input (ab)3(bc)3(ca)3 Step by step solution Step 1 11 Evaluate (ca)3 = c33ac23a2ca3 Step 2 Pulling out like terms 21Prove that (a b c)^3 a^3 b^3 c^3 = 3 (a b ) (b c) (c a) untaggedFor the logical argument 1 ~A v ~B 2 A > B 3 C > (D > A) therefore c ~C v ~D is this logical proof correct?

Inequalities Marathon

Methods Of Proof Lecture 4 Sep 16 Chapter 3 Of The Book Ppt Download

Multiply (dot product) † by A to get, A ( A × ( B × C)) = α ( A B) − β ( A C) Since A ( A × ( B × C)) = ( A \ti Continue Reading B × C is a vector purpendicular to the plane formed by B and C Hence the vector A × ( B × C) lies in the plane formed by B and CThe LibreTexts libraries are Powered by MindTouch ® and are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot We also acknowledge previous National Science Foundation support under grant numbers , , andQuite unfortunately not from the simple perspective requested, I have found that P = a 3 b 3 c 3 3abc = 2S, where S is the area of the triangle of vertices

Prove Consequences Of The Field Axioms Stumbling Robot

2

What the rule says is this if have a disjunction in a proof, and you have shown, through a sequence of subproofs, that each of the disjuncts (together with any other premises in the main proof) leads to the same conclusion, then you may derive that conclusion from the disjunction (together with any main premises cited within the subproofs)Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3 (2a) (3b) (5c) And this represents identity a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5cCalculate squares 1 1 = c2 11=2 2 = c2 Swap sides c2 = 2 Square root of both sides c = √2 Which is about c = It works the other way around, too when the three sides of a triangle make a2 b2 = c2, then the triangle is right angled

Answered 76 Chapter 2 Sets And Whole Numbers 11 Bartleby

Exercises For Chapter 7 1 Prove If Gcd A B C Then Gcd B2 C2

Asked Jan 30, 18 in Class IX Maths by ashu Premium (930 points) Prove that (a b c) 3 a 3 b 3 – c 3 =3 (a b) (b c) (c a) polynomialsProve using conditional proof 1 1 A B C 2 B E 3 C E X A X Answer 4 A ACP 5 B C from ENG 6301 at Mapúa Institute of Technology4 A > (A & B) (2, absorption) 5 ~A (4,1 Modus Tollens) 6 C > (D > (A & B)) (3,4 Hypothetical Syllogism) 7 C > ~D (6,5 Modus Tollens) 8 C > (~D v ~C) (7, Addition) 9 ~C > (~C v ~D) (Add) c ~C v ~D (8,9) I am relatively new to logical proofs, and i'm not sure I can

Proof Of Pappus S Theorem If A B C Are 3 Collinear Points As Well Download Scientific Diagram

If A B C Are In Ap Prove That A 3 C 3 6abc 8b 3 Brainly In

Prove using conditional proof 1 1 A B C 2 B E 3 C E X A X Answer 4 A ACP 5 B C from ENG 6301 at Mapúa Institute of TechnologyTheorem For any sets A and B, A−B = A∩ Proof We must show A− B ⊆ A∩ and A ∩ ⊆ A−B First, we show that A −B ⊆ A ∩ Let x ∈ A− B By definition of set difference, x ∈ A and x 6∈B By definition of complement, x 6∈B implies that x ∈ Hence, it is true that both, x ∈ A and x ∈(8) Multiplication distributes over addition a(bc)=abac and (ab)c = acbc Other possible properties are captured by special types of rings We will encounter many in this book;

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

Q Tbn And9gcsectilf2waloldhrvvptyk0gppw0kxl9fe R8 Qft5iyl5p4g2 Usqp Cau

Proof RHS dec v v a v a 1 bv a 2 a b 1R c Law 974 unfold dec v v a v a1 a b 1 R Proof rhs dec v v a v a 1 bv a 2 a b 1r c law 974 School Daffodil International University (Campus 2) Course Title MATH MISC;For the logical argument 1 ~A v ~B 2 A > B 3 C > (D > A) therefore c ~C v ~D is this logical proof correct?3 Let A, B, C be subsets of the universal set U Justify each answer with a proof or counterexample, as appropriate Note that a counterexample consists of a universe and a collection of sets for which the given statement is false;

If A B C Then B A Cup C Mathematics Stack Exchange

2

(A and B) A or B De Morgan's law for \and" A )(B )C) (A and B) )C conditional proof In a course that discusses mathematical logic, one uses truth tables to prove the above tautologies 2 Sets A set is a collection of objects, which are called elements or members of the set Two sets are equal when they have the same elements Common SetsProve that (AB)C= (AC) (BC) Let A,B and C be sets Prove that (AB)C= (AC) (BC) Suppose x ∈ ( A − B) − C Since x ∈ ( A − B) − C this means that x ∈ A but x ∉ B and x ∉ C I'm not sure how to show how these two statements are equalDirect proof could include x∈ Q in the antecedent Solution The three forms are 1 (Direct) If a,b,c are odd, then, for all x∈ Q, ax2 bxc 6= 0 1 (Direct) If a,b,c are odd and x∈ Q, then ax2 bxc 6= 0 2 (Contrapositive) Suppose a,b,c∈ Z If there exists x∈ Q such that ax2 bxc = 0, then at least one of a,b,c is even 3

What Are Various Forms To Write A B C A Whole Cube Quora

2

We can choose an a in 3 ways, and then a b in 2 ways, and then we have only one way to choose a c The coefficient is therefore 3·2·1=6 Finally, add up the coefficients to check they come to (111) 3 =27But maybe x is in A C not a problem, B∩C is a subset of C, as well, so x not being in C excludes it from being in any subset of C, including the subset B∩C, so in all cases, we see x is in A, but not in B∩C, so x is in A (B∩C), so (A B) U (A C) is a subset of A (B∩C) as well, and the two sets must therefore be equalWRITE THE PROOF THEOREM Let a, b, and c be integers with a \ne 0 and b \ne 0 If ab and bc, then ac PROOF Suppose a, b, and c are integers where both a and b do not equal to zero Since a divides b, ab, then there exists an integer m such that b = am (Equation #1) Similarly, since b divides c, bc, there exists an integer n such that c=bn (Equation #2)

Proof Of 501 C 3 Warrior Outdoors

2

If the scalar triple product is equal to zero, then the three vectors a, b, and c are coplanar, since the parallelepiped defined by them would be flat and have no volume If any two vectors in the scalar triple product are equal, then its value is zeroNow we'll use it in a proof 1 A ( C 2 A 3 B 4 C ( Elim 1, 2 5 (A ( B) ( C ( Intro 24 What's going on here is that because we modified our rule, A and B can both be assumptions, indicated by the fact that they are above the Fitch bar (The first horizontal Fitch bar indicates that A ( C is a premise)Summary (abc)^2 If you have any issues in the (abc)^2 formulas, please let me know through social media and mail A Plus B Plus C Whole Square is most important algebra maths formulas for class 6 to 12

Solved For Each Proof You Must Include I E Write The Chegg Com

2

Uploaded By MinisterAntelope19 Pages 466 This preview shows page 292 295 out of 466 pagesProve (true) that for all sets A and B, (A ∪ B) c = A c ∩ B c Proof Skeleton only We must show that (A ∪ B) c ⊆ A c ∩ B c and that A c ∩ B c ⊆ (A ∪ B) c To show the first containment means to show that ∀∀∀∀x, if x ∈∈∈∈ (A ∪∪∪∪ B) c then x ∈∈∈∈ A c ∩ B cThe left hand side proof is tricky but here it is, although it would be much easier to use the right hand side given a^3 b^3 c^3 3abc factor a^3 b^3 using cubic formula (ab) (a^2 ab

2 When Is A 2 Digit Number The Sum Of The Squares Of Its Digits Pdf Free Download

Cseweb Ucsd Edu Classes Sp09 Cse140 Mid1samp Sol Pdf

Many more are studied as well by mathematicians Theorem 33 Additive inverses are unique Proof Assume that x and y are both inverses of aThenx=x0=x(ay)= (xa)y=0y=yMATHEMATICAL FORMULAE Algebra MATHEMATICAL FORMULAE Algebra 1 (ab)2=a22abb2;a2b2=(ab)2−2ab 2 (a−b)2=a2−2abb;a2b2=(a−b)22ab 3 (abc)2=a2b2c22(abbcca) 4 (ab)3=a3b33ab(ab);a3b3=(ab)−3ab(ab) 5What the rule says is this if have a disjunction in a proof, and you have shown, through a sequence of subproofs, that each of the disjuncts (together with any other premises in the main proof) leads to the same conclusion, then you may derive that conclusion from the disjunction (together with any main premises cited within the subproofs)

Solved Let A B And C Be Sets Present A Direct Proof For Chegg Com

Math Garden Morley S Theorem

4 A > (A & B) (2, absorption) 5 ~A (4,1 Modus Tollens) 6 C > (D > (A & B)) (3,4 Hypothetical Syllogism) 7 C > ~D (6,5 Modus Tollens) 8 C > (~D v ~C) (7, Addition) 9 ~C > (~C v ~D) (Add) c ~C v ~D (8,9) I am relatively new to logical proofs, and i'm not sure I canAn Alternative Sine Rule Proof a/sinA = b/sinB = c/sinCVideo by Tiago Hands (https//wwwinstagramcom/tiago_hands/)Instagram ResourcesMathematics ProofsQuestion Write A Proof For The Arguments 1 E⊃F ∴ ~F⊃~E 2 ~A V ~B B V ~C ∴ A ⊃ ~C 3 (A V B) & ~(A & B) A V C ~(B & C) ∴ ~B & A This problem has been solved!

Www Math Lsu Edu Adkins M4181 4181f19ps3a

Solved 1 21 Prove That A B C 3 A3 C3 3 A B Chegg Com

Www Math Tamu Edu Boggess Math222 Hwsolutions Sampleproof Pdf

Sample Problems

Http Www Math Lsa Umich Edu Kesmith Cosets Pdf

2

Prove That Tex A B C 3 A 3 B 3 C 3 3 A B B C C A Tex Brainly In

Http Www Thebookshelf Auckland Ac Nz Docs Maths Pdf Mathschron004 003 Pdf

Prove The A B C 3 A 3 B 3 C 3 3 A B B C C A Brainly In

Prove That There Do Not Exist Prime Numbers A B And C Such That A 3 B 3 C 3 Prove It By Using The 4 Cases Use A Correct And Complete English Sentence

2

2

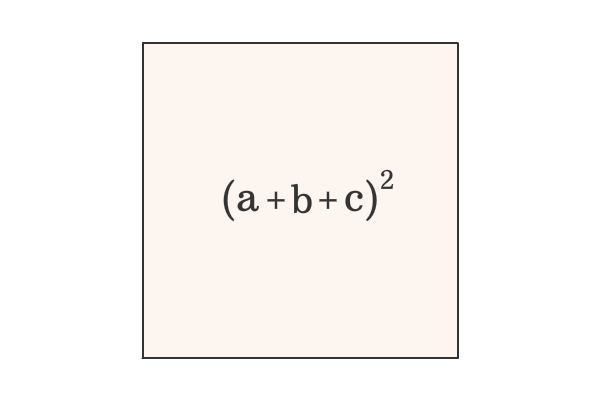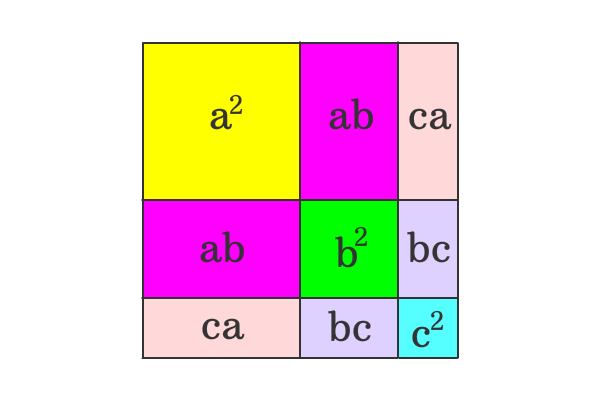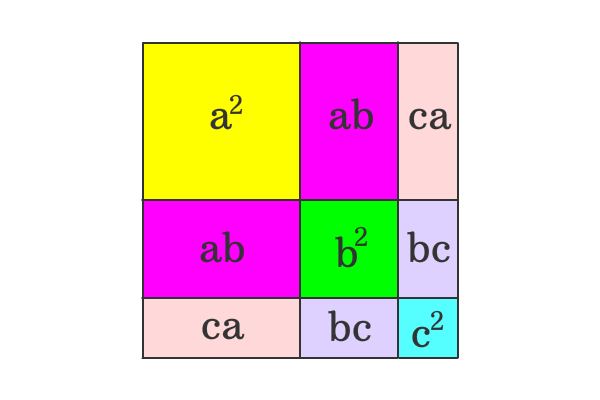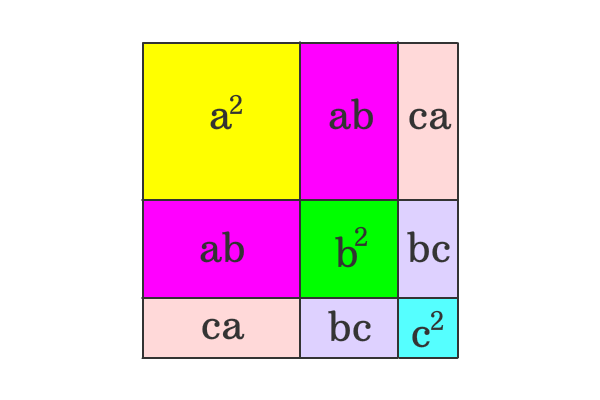
Proof Of A B C Formula In Geometric Method

Condor Depaul Edu Ntomuro Courses 400 Notes Lecture4 Pdf

Openresearch Repository Anu Edu Au Bitstream 15 2 B Gupta C K Pdf

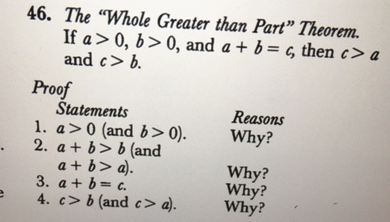
The Whole Greater Than Part Theorem If Math A Gt0 Math Math B Gt0 Math And A B C Then Math C Gt A Math And Math C Gt B Math Proof Math Begin Array Ll Text Statements Text Reasons 1 A Gt0 Text And B Gt0 Text Why

Solved Here Is A Proof That 3 4 Let A B And C Be Any T Chegg Com

2

2 5 Proving Statements About Segments Ppt Video Online Download

2

Vector Analysis By Alimkanwalimtinaa Issuu

Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube

2

What Is The Expansion Of A B C 3 Quora

What Is The First Line Of The Proof 1 If A Divides B Then A Divides B C 2 If A Divides B Then A Divides C 3 Assume A Divides

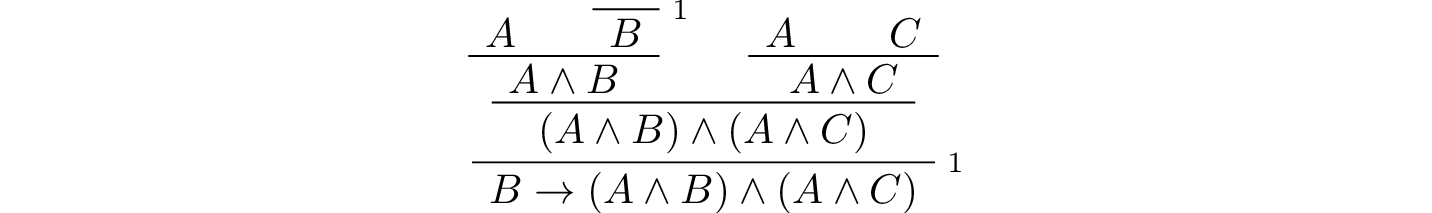
3 Natural Deduction For Propositional Logic Logic And Proof 3 18 4 Documentation

A 3 B 3 C 3 3abc Formula A B 2 A 2 B 2 2ab Proof Derivation Of Algebraic Identities Youtube Youtube

Prove A B C 3 A 3 B 3 C 3 3 A B B C C A Mathematics Topperlearning Com 9j3ovqff

Http Oregonstate Edu Instruct Mth341 Garity Fall00 Section1 4 Pdf

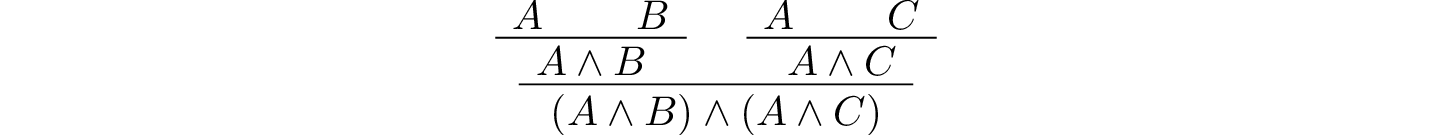
3 Natural Deduction For Propositional Logic Logic And Proof 3 18 4 Documentation

22 Prove If A B And C Are Odd And A B C And A Then A B And A C 22 Prove If A B And C

Faculty Math Illinois Edu Rtramel Math418spring17hw4 Pdf

2

A B C 3 Formula Proof

Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube

Arxiv Org Pdf 1509

How Do I Prove 1 A V B C 2 A V C G O G V O Philosophy Stack Exchange

2

2

Http Www Thebookshelf Auckland Ac Nz Docs Maths Pdf Mathschron004 003 Pdf

A3

A B C 3 Formula Proof

2

Www Cs Uaf Edu Faudree M401h7s Pdf

Web Maths Unsw Edu Au Mikeh Webpapers Paper98 Pdf

Ppt Chapter 3 Homework Review Exercises 2 7 2 3 6 7 Are Correct Powerpoint Presentation Id

A B C 3

2

Solved 12 Evaluation Of Proofs See The Instructions For Chegg Com

2

Http Granite Sru Edu Lmiller Course Materials 3 Zhw 3 Sol05 S08 Pdf

2

The Inequality Frac A 4 A 3 B 3 Frac B 4 B 3 C 3 Frac C 4 C 3 A 3 Ge Frac A B C 2 Mathematics Stack Exchange

Nanopdf Com Download Math 431 Homework 4 Due 10 13 Pdf

What Is The Formula For Math A B C 3 Math Quora

Www Cs Csustan Edu Mmartin Teaching Math2300s16 Homework 2300 Ch5 Homework Pdf

Natural Deduction Proof For A To B To C To A To B To A To C Mathematics Stack Exchange

Two Column Proofs Given 2x 3 2 3 Prove X 11 6 Statements Ppt Download

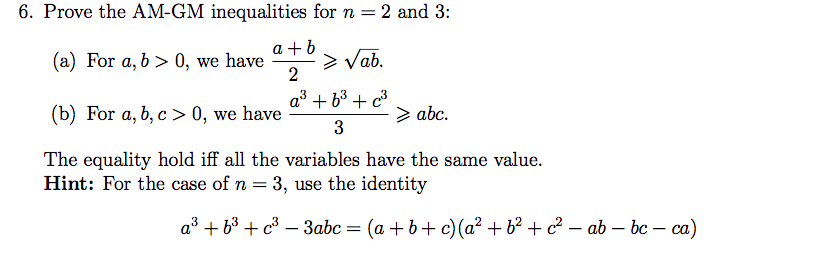
Solved 6 Prove The Am Gm Inequalities For N 2 And 3 T Chegg Com

Http Users Math Msu Edu Users Robertbe Mth310sp11homework S3 Pdf

Proof That Metric Spaces Are Paracompact

Http Btravers Weebly Com Uploads 6 7 2 9 Problem Set 3 Solutions Pdf

Example 6 Prove That A 3 B 3 C 3 3abc 1 2 A B C A B

Search Q A 5e3 2bb 5e3 2bc 5e3 3abc Tbm Isch

2

2

Search Q A 5e3 2bb 5e3 2bc 5e3 Formula Tbm Isch

Prove That A B C 3 A3 C3 3 A B B C C A Math Polynomials Meritnation Com

Inequalities Marathon

2

Inequalities From The Word 1995 05

A 3 B 3 C 3 3abc Formula Proof

Http Math Bu Edu People Rpollack Teach 129fall10 129midterm1 Solns Pdf

Www Math Fsu Edu Hoeij Spring19 Mgf3301 Sampletests Test2fall15answers Pdf

Incoming Term: (a+b+c)^3 proof, (a+b+c)^3 formula proof, a^3+b^3+c^3-3abc proof, a^3+b^3+c^3-3abc formula proof,